问题
问答题
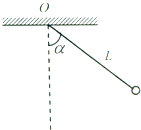
如图所示,质量为m的小球,用长为L的细线悬挂在水平天花板上的O点.现将小球偏离平衡位置,使细线与竖直方向的夹角为α,然后将小球由静止释放.当小球运动到最低点时,试求:
(1)小球的速度大小;
(2)小球的角速度大小;
(3)小球对细线拉力的大小.
(已知当地的重力加速度为g,不计空气阻力)
答案
(1)设球由静止释放运动到最低点时的速度大小为v,根据机械能守恒定律得:
mgL(1-cosα)=
mv21 2
解得:v=2gL(1-cosα)
(2)根据v=ωL
联立解得小球的角速度大小ω=2gL(1-cosα) L
(3)设在最低点细线对小球拉力的大小为T,根据牛顿第二定律得:
T-mg=mv2 L
解得:T=(3-2cosα)mg
根据牛顿第三定律,小球对细线拉力的大小
Tˊ=T=(3-2cosα)mg
答:(1)小球的速度大小为
;2gL(1-cosα)
(2)小球的角速度大小为
;2gL(1-cosα) L
(3)小球对细线拉力的大小为(3-2cosα)mg.
