问题
计算题
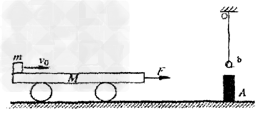
如图所示，一质量为M=3.0kg的平板车静止在光滑的水平地面上，其右侧足够远处有一障碍物A，质量为m=2.0kg的b球用长l=2m的细线悬挂于障碍物正上方，一质量也为m的滑块(视为质点)，以υ0=7m ／s的初速度从左端滑上平板车，同时对平板车施加一水平向右的、大小为6N的恒力F，当滑块运动到平板车的最右端时，二者恰好相对静止，此时撤去恒力F。当平板车碰到障碍物A时立即停止运动，滑块水平飞离平板车后与b球正碰并与b粘在一起。已知滑块与平板车间的动摩擦因数μ=0.3，g取10m／s2，求：
(1)撤去恒力F前，滑块、平板车的加速度各为多大，方向如何？
(2)撤去恒力F时，滑块与平板车的速度大小。
(3)悬挂b球的细线能承受的最大拉力为50N，a、b两球碰后，细线是否会断裂？(要求通过计算回答)
答案
解：(1)对滑块，由牛顿第二定律得：a1=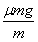
=μg=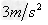
，方向水平向左
对平板车，由牛顿第二定律得：a2=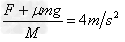
，方向水平向右
(2)设经过时间t1滑块与平板车相对静止，此时撤去恒力F，共同速度为v1
则：v1=v0-a1t1，v1=a2t1
解得：t1=1s，v1=4m ／s
(3)滑块与小球碰撞，动量守恒：mv1=2mv2
解得v2=2m／s
设细线拉力为T，T-2mg=2m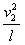
T=2mg+2m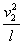
代入数值得：T=48N<50N，细线不会断裂