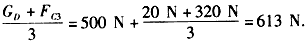某工人用如图所示的组合机械打捞浸在水中密度为8×103 kg/m3的金属块A,杠杆BC可绕O点在竖直平面内转动,OB: OC =1:2,工人受到的重力为500 N。当金属块A有3/4的体积露出水面时,杠杆在水平位置平衡,工人对工作台的压力为F1;从进水口中向容器中注水,当金属块A全部浸没在水中 时,容器底部受到水的压力变化了60 N,杠杆仍在水平位置平衡,工人对工作台的压力为F2。已知F1:F2= 61: 60,杠杆BC和细绳的质量、滑轮间的摩擦均忽略不计,g= 10 N/kg,求:
(1)动滑轮D受到的重力GD;
(2)当金属块全部脱离水面时,杠杠在水平位置再次平衡,此时工人对工作台的压力F3是多大?(结果保留整数)
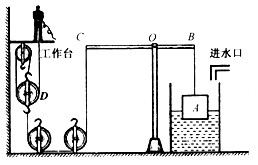
解:
(1)容器底部受到的液体压力的变化等于A受到的浮力的变化,即
ΔF压=ΔF浮=ρ水gΔV排=1.0×103kg/m3×10N/ kg×(3/4)VA =60 N,
解得:VA=8×10-3m3。
物体A受到的重力为:
GA=ρAgVA =8×103kg/m3×10 N/ kg 8×10-3m3=640N,
F浮A=ρ水g(1/4)VA=1.0×103 kg/m3 ×10 N/kg×2×10-3m3= 20 N,
F浮A'=ρ水gVA=l.0×103kg/m3×10N/kg×8×10-3m3=80N。
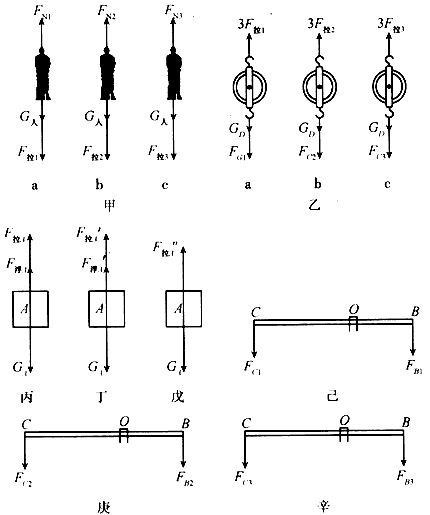
由于物体平衡,则由力的示意图丙、丁有:
F拉A=GA- F浮A= 640 N-20 N =620N,F拉A= FB1,F拉A'= GA - F浮A'= 640 N -80 N =560 N,F拉A'= FB2
根据杠杆平衡条件,由图己、庚有:
FC1×LOC= FB1×LOB,LOB: LOC =1:2,解得:FC1 =310 N
FC2×LOC= FB2×LOB,LOB: LOC=1:2,解得:FC2=280 N.
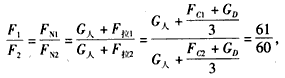
GD= 20N;
(2)F3=FN3=G人+F拉3=G人+