问题
问答题
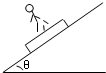
如图所示,质量为M的木板可沿倾角为θ的光滑斜面下滑,木板上站着一个质量为m的人,问
(1)为了保持木板与斜面相对静止,计算人运动的加速度?
(2)为了保持人与斜面相对静止,木板运动的加速度是多少?
答案
(1)为了使木板与斜面保持相对静止,必须满足木板在斜面上的合力为零,所以人施于木板的摩擦力F应沿斜面向上,故人应加速下跑.现分别对人和木板应用牛顿第二定律得:
对木板:Mgsinθ=F.
对人:mgsinθ+F=ma人(a人为人对斜面的加速度).
解得:a人=
gsinθ,方向沿斜面向下.M+m m
(2)为了使人与斜面保持静止,必须满足人在木板上所受合力为零,所以木板施于人的摩擦力应沿斜面向上,故人相对木板向上跑,木板相对斜面向下滑,但人对斜面静止不动.现分别对人和木板应用牛顿第二定律,设木板对斜面的加速度为a木,则:
对人:mgsinθ=F.
对木板:Mgsinθ+F=Ma木.
解得:a木=
gsinθ,方向沿斜面向下.M+m M
即人相对木板向上加速跑动,而木板沿斜面向下滑动,所以人相对斜面静止不动.
答:(1)为了保持木板与斜面相对静止,人运动的加速度为
gsinθ,方向沿斜面向下.M+m m
(2)为了保持人与斜面相对静止,木板运动的加速度是
gsinθ,方向沿斜面向下.M+m M
