问题
问答题
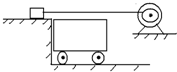
如图所示,质量为M的小车静止在光滑的水平面上,质量为m的小滑块在电动机的牵引下以恒定的速度向前运动,现使小滑块滑到小车上,经过一段时间后,m与M处于相对静止,从小滑块滑到小车到与小车相对静止的整个过程中小滑块的速度始终保持为v不变,它与小车之间的动摩擦因数为μ,求:
(1)在这段时间内,小车的位移是多少?
(2)这个过程电动机的牵引力做的功是多少?
(3)这个过程滑块与小车之间产生的热量为多少?
答案
(1)设小滑块在小车上的滑动摩擦力为Ff,
则Ff=μmg
根据牛顿第二定律有:Ff=Ma,则a=μmg M
从小滑块滑上小车到相对小车静止所经历的时间为t,则t=
=v a
.Mv μmg
因为小车做匀加速直线运动,所以小车的位移x=
?t=v 2
. Mv2 2μmg
(2)在这段过程中,牵引力等于摩擦力,牵引力做的功为:
W=Ffvt=M v2
(3)对系统由能量关系有W=Q+EK=Q+
Mv21 2
得整个过程中滑块与小车之间产生热量 Q=
Mv2.1 2
答:(1)在这段时间内,小车的位移是
.Mv2 2μmg
(2)这个过程电动机的牵引力做的功是M v2.
(3)这个过程滑块与小车之间产生的热量为
Mv2.1 2
