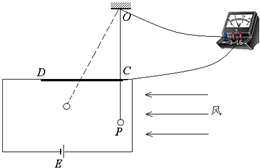
某研究性学习小组,为了探索航天器球形返回舱穿过大气层时所受空气阻力(风力)的影响因素,进行了模拟实验研究.如图为测定风力的实验装置图,其中CD是一段水平放置的长为L的光滑均匀电阻丝,电阻丝电阻较大;一质量和电阻都不计的细长细长裸金属丝一端固定于O点,另一端悬挂球P,无风时细金属丝竖直,恰与电阻丝在C点接触,OC=H;有风时金属丝将偏离竖直方向,与电阻丝相交于某一点(如图中虚线所示).细金属丝与电阻丝始终保持良好的导电接触.
(1)已知电源的电动势为E,内阻不计,理想电压表两接线柱分别与O点和C点相连,球P的质量为m,重力加速度为g,由此可以推得风力大小F与电压表示数的关系式为F=______.
(2)研究小组的同学猜想:风力大小F可能与风速大小v和球半径r这两个因素有关,于是他们进行了如下的实验:
实验一:使用同一球,改变风速,记录了在不同风速下电压表的示数.
表一 球半径r=0.50cm
| 风速(m/s) | 10 | 15 | 20 | 30 |
| 电压表示数(V) | 2.40 | 3.60 | 4.81 | 7.19 |
实验二:保持风速一定,换用同种材料、不同半径的实心球,记录了在球半径不同情况下电压表的示数.
表二 风速v=10m/s
| 球半径(cm) | 0.25 | 0.50 | 0.75 | 1.00 |
| 电压表示数(V) | 9.60 | 2.40 | 1.07 | 0.60 |
| 4 |
| 3 |
(3)根据上述实验结果可知风力的大小F与风速大小v、球半径r的关系式为______.
(1)以小球为研究对象,对小球进行受力分析,设小球受到风力为F是细金属丝与竖直方向的夹角为θ,由平衡条件可知其风力
F=mgtanθ ①
设细金属丝与电阻丝相交点与C点之间的长度Htanθ,电阻为R′=
Htanθ,R L
由串联电路的分压规律可知电压表示数 U=
=ER′ R
Htanθ ②E L
①②两式联立解得 F=
U ③mgL EH
(2)由表一中的测量数据可以看出,在球半径一定的情况下,风力大小与风速成正比,即F与v成正比.
由表二中的测量数据可知:在风速一定的情况下,球半径增大到原来的二倍,电压表示数减小为原来的
.1 4
由③式和球体积公式、密度公式可得 F=
U=mgL EH
U=VρgL EH
?ρgL EH
πr3U4 3
综合考虑可得在风速一定的情况下,风力大小与球半径的关系是:F与r成正比.
(3)根据上述两次实验结果可以得出,风力大小与风速成正比,与球半径成正比,风力的大小F与风速大小v、球半径r的关系式可以写为F=kvr,式中k为常数.
故答案为:
(1)F=
UmgL EH
(2)风力大小与风速成正比
(3)F=kvr,式中k为常数.
