问题
问答题
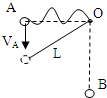
如图所示,长为L的轻质细绳一端系于固定点O,另一端系一个质量为m的小球,现让小球在O点左侧同一高度,离O点距离为
L的A点,以初速度vA=3 2
竖直向下抛出.经一定时间后细绳被拉直,以后小球将以O为圆心在竖直平面内摆动,求:小球抛出后到达最低点B时的加速度.gL
某同学解答如下:
根据机械能守恒定律,取小球到达最低点位置为零势能点,则下抛时机械能等于最低点时的机械能,mgL+
mvA2=1 2
mvB2; 先求出B点的速度,再求出B点的加速度.1 2
你认为该同学的解答思路是否正确?如果正确请算出最后结果;如果认为错误,请用正确的方法求出结果来.
答案
解(1)不正确
当绳子被拉直时,小球的机械能要损失
(2)正确解法:设刚拉直位置为C点;
小球从下抛到刚拉直前机械能守恒,小球下降高度为 L 2
mg
+L 2
m1 2
=v 2A
m1 2 v 2c
vc=2gL
在绳子拉直的瞬间,小球沿绳子方向的速度变为零,只剩下垂直于绳子方向的分速度.
所以 v′c=vccos30°=6gL 2
接下来到达最低点B的过程中机械能守恒:mg
+L 2
mv1 2
=′ 2c
m1 2 v 2B
vB=
gL5 2
则a=
=v2 L 5g 2
答:不正确,小球抛出后到达最低点B时的加速度为
.5g 2
