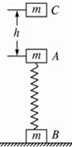
如图所示,质量均为m的两物体A、B分别与轻质弹簧的两端相连接,将它们静止放在地面上.一质量也为m的小物体C从距A物体h高处由静止开始下落.C与A相碰后立即粘在一起向下运动,以后不再分开.当A与C运动到最高点时,物体B对地面刚好无压力.不计空气阻力.弹簧始终处于弹性限度内.已知重力加速度为g.求
(1)A与C一起开始向下运动时的速度大小.
(2)A与C一起运动的最大加速度大小.
(3)弹簧的劲度系数.(提示:弹簧的弹性势能只由弹簧劲度系数和形变量大小决定)
(1)设小物体C从静止开始运动到A点时的速度为v,由机械能守恒定律有:
mgh=
mv21 2
设C与A碰撞粘在一起的速度为v′,由动量守恒定律得,
mv=(m+m)v′,
解得v′=1 2
.2gh
答:A与C一起开始向下运动时的速度大小为1 2
.2gh
(2)A与C一起将在竖直方向上做简谐运动.当A与C运动到最高点时,回复力最大,加速度最大、
AC、B受力如图.
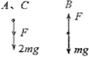
B受力平衡有:F=mg
对AC运用牛顿第二定律:F+2mg=2ma
解得a=1.5g.
答:A与C一起运动的最大加速度大小为1.5g.
(3)设弹簧的劲度系数为k
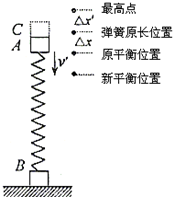
开始时A处于平衡状态,设弹簧的压缩形变量为△x
对A有k△x=mg①
当A与C运动到最高时,设弹簧的拉伸形变量为△x″
对B有k△x″=mg②
由以上两式得△x=△x″
因此,在这两个位置时弹簧的弹性势能相等:
对A、C,从原平衡位置到最高点,根据机械能守恒定律
E弹+
(m+m)v′2=2mg(△x+△x″)+E弹′③1 2
联立各式解得:k=8mg h
答:弹簧的劲度系数为
.8mg h
