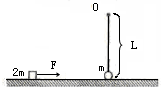
如图所示,长为L的不可伸长的绳子一端固定在O点,另一端系质量为m的小球,小球静止在光滑水平面上.现用大小为F水平恒力作用在另一质量为2m的物块上,使其从静止开始向右运动,一段时间后撤去该力,物块与小球发生正碰后速度变为原来的一半,小球恰好能在竖直平面内做圆周运动.已知重力加速度为g,小球和物体均可视为质点,试求:
(1)小物块碰撞前速度V0的大小;
(2)碰撞过程中系统损失的机械能;
(3)恒力F作用时间.
(1)小球恰好通过最高点作圆周运动,此时重力刚好提供向心力,设速度为V,有
mg=mV2 L
得V=gL
设小球碰撞后速度为V1,其后在摆至最高点过程中,机械能守恒:
mV12=1 2
mV2+mg•2L 1 2
代入V值可得V1=5gL
碰撞过程中,物块和小球系统动量守恒,有
2mV0=mV1+2m•V0 2
代入V1值可得V0=5gL
(2)碰撞过程中系统损失的机械能
△E=
•2m•V02-1 2
•2m•(1 2
)2-V0 2
mV121 2
代入所求出的速度值可得
△E=
mgL 5 4
(3)小球在水平面运动的加速度a=F 2m
由速度公式V0=at得力F作用时间
t=
=V0 a 2m 5gL F
答:(1)小物块碰撞前速度V0的大小是
;5gL
(2)碰撞过程中系统损失的机械能是
mgL;5 4
(3)恒力F作用时间是
.2m 5gL F
