问题
问答题
质量为M的拖拉机拉着耙来耙地,由静止开始做匀加速直线运动,在时间t内前进的距离为s.耙地时,拖拉机受到的牵引力恒为F,受到地面的阻力为自重的k倍,耙所受阻力恒定,连接杆质量不计且与水平面的夹角θ保持不变.求:
(1)拖拉机的加速度大小.
(2)拖拉机对连接杆的拉力大小.
(3)时间t内拖拉机对耙做的功.

答案
(1)拖拉机在时间t内匀加速前进s,根据位移公式,
x=
at2=s ①1 2
解得:a=
②2s t2
(2)设连接杆对拖拉机的拉力为T,对拖拉机受力分析:
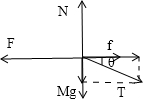
由牛顿第二定律得,F-kMg-Tcosθ=Ma ③
由②③联立得T=
④F-M(kg+
)2s t2 cosθ
根据牛顿第三定律知,拖拉机对连接杆的拉力大小为T′=T=
⑤F-M(kg+
)2s t2 cosθ
(3)拖拉机对耙所做的功就是通过连接杆的拉力对耙做功.故拖拉机对耙做的功,W=T'scosθ ⑥
由⑤⑥两式得w=[F-M(kg+
)]s2s t2
答:(1)拖拉机的加速度大小是
.2s t2
(2)拖拉机对连接杆的拉力大小是
.F-M(kg+
)2s t2 cosθ
(3)时间t内拖拉机对耙做的功是[F-M(kg+
)]s.2s t2
