问题
问答题
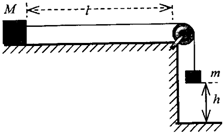
如图所示,水平平台的右端安装有滑轮,质量为M的物块放在与滑轮相距l的平台上,物块与平台间的动摩擦因数为μ现有一轻绳跨过定滑轮,左端与物块连接,右端挂质量为m的小球,绳拉直时用手托住小球使其在距地面h高处静止,重力加速度为g.设最大静摩擦力等于滑动摩擦力(g取10m/s2).
(1)放开小球,系统运动,求小球做勾加速运动时的加速度及此时绳子的拉力大小.
(2)设M=2kg,l=2.5m,h=0.5m,μ=0.2,小球着地后立即停止运动,要使物块不撞到定滑轮,则小球质量m应满足什么条件?
答案
(1)由牛顿第二定律得
对小球:mg-F=ma
对物块:F-μMg=Ma
联立解得a=mg-μMg M+m
F=(1+μ)Mmg M+m
(2)小球落地时速度为v=2ah
对物块:根据动能定理得,
-μMgs=0-
Mv21 2
其中s≤l-h
联立解得,a≤8m/s2
又因为a=
,得m≤10kgmg-μMg M+m
要能拉动物块必须有mg>μMg,即m>0.4kg
所以小球 质量范围为0.4kg<m≤10kg
答:
(1)小球做勾加速运动时的加速度为
,此时绳子的拉力大小为mg-μMg M+m
.(1+μ)Mmg M+m
(2)要使物块不撞到定滑轮,小球质量m应满足0.4kg<m≤10kg.
