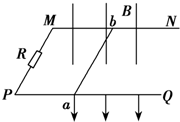
如图所示,两根光滑的平行金属导轨MN、PQ处于同一水平面内,相距L=0.5m,导轨的左端用R=3Ω的电阻相连,导轨电阻不计,导轨上跨接一电阻r=1Ω的金属杆ab,质量m=0.2kg,整个装置放在竖直向下的匀强磁场中,磁感应强度B=2T,现对杆施加水平向右的拉力F=2N,使它由静止开始运动,求:
(1)杆能达到的最大速度为多大?最大加速度为多大?
(2)杆的速度达到最大时,a、b两端电压多大?此时拉力的瞬时功率多大?
(3)若已知杆从静止开始运动至最大速度的过程中,R上总 * * 生了10.2J的电热,则此过程中拉力F做的功是多大?此过程持续时间多长?
(4)若杆达到最大速度后撤去拉力,则此后R上 * * 生多少热能?其向前冲过的距离会有多大?
(1)由题意得匀速运动时速度最大,此时有:F=BIL
F=
,v=8 m/s B2L2v R+r
刚开始运动时加速度最大,a=
=10 m/s2 F m
(2)由欧姆定律得:Uab=
R=6 V BLv R+r
拉力的瞬时功率为 P=F•v=16 W
(3)由能量转化和守恒关系得:Fs=
mv2+QR+Qr=20J,1 2
其中 Qr=
QR r R
代入得s=10 m
根据动量定理得
mv=Ft-B
Lt. I
又
t=q. I
感应电量q=
=△Φ R+r B•Ls R+r
联立得:mv=Ft-B2L2s R+r
代入解得 t=2.05 s
(4)
mv2=QR+Qr=QR+1 2
QR1 3
代入得QR=4.8 J
mv=BILt′=BL
=△Φ R+r B2L2s′ R+r
代入得s′=6.4 m
答:
(1)杆能达到的最大速度为8 m/s,最大加速度为10 m/s2.
(2)杆的速度达到最大时,a、b两端电压是6V,此时拉力的瞬时功率为16 W.
(3)拉力F做的功是20J,此过程持续时间是2.05 s.
(4)R上 * * 生4.8J热能,其向前冲过的距离会有6.4 m.
