问题
问答题
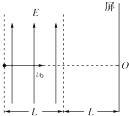
如图所示,在两条平行的虚线内存在着宽度为L、场强为E的匀强电场,在与右侧虚线相距也为L处有一与电场平行的屏.现有一电荷量为+q、质量为m的带电粒子(重力不计),以垂直于电场线方向的初速度v0射入电场中,v0方向的延长线与屏的交点为O.试求:
(1)粒子在电场中运动的时间;
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tanα;
(3)粒子打到屏上的点P到O点的距离Y.
答案
(1)粒子在垂直于电场线的方向上做匀速直线运动,则粒子在电场中运动的时间的时间t=
.L v0
(2)设粒子射出电场时沿平行电场线方向的速度为vy,根据牛顿第二定律,粒子在电场中的加速度为:a=qE m
所以vy=at=a
=L v0 qEL mv0
所以粒子刚射出电场时的速度方向与初速度方向间夹角的正切值为tanα=
=vy v0
.qEL m v 20
(3)设粒子在电场中的偏转距离为y,则y=
at2=1 2
•1 2
t2qEL mv0
又Y=y+Ltanα
解得:Y=3qEL2 2m v 20
答:
(1)粒子在电场中运动的时间是
;L v0
(2)粒子刚射出电场时的速度方向与初速度方向间夹角的正切值tanα为
;qEL m v 20
(3)粒子打到屏上的点P到O点的距离Y是
.3qEL2 2m v 20
