如图所示,劲度系数为k=200N/m的轻弹簧一端固定在墙上,另一端连一质量为M=8kg的小车a,开始时小车静止,其左端位于O点,弹簧没有发生形变,质量为m=1kg的小物块b静止于小车的左侧,距O点s=3m,小车与水平面间的摩擦不计,小物块与水平面间的动摩擦系数为μ=0.2,取g=10m/s2.今对小物块施加大小为F=8N的水平恒力使之向右运动,并在与小车碰撞前的瞬间撤去该力,碰撞后小车做振幅为A=0.2m的简谐运动,已知小车做简谐运动周期公式为T=2π
,弹簧的弹性势能公式为Ep=M k
kx2(x为弹簧的形变量),则1 2
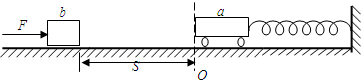
(1)小物块与小车磁撞前瞬间的速度是多大?
(2)小车做简谐运动过程中弹簧最大弹性势能是多少?小车的最大速度为多大?
(3)小物块最终停在距O点多远处?当小物块刚停下时小车左端运动到O点的哪一侧?
(1)设磁撞前瞬间,小物块b的速度为v1
小物块从静止开始运动到刚要与小车发生碰撞的过程中,
根据动能定理可知
Fs-μmgs=
mv1…•①1 2
解得v1=6m/s…②
(2)由于小车简谐振动的振幅是0.2m,所以弹簧的最大形变量为x=A=0.2m
根据弹性势能的表达式可知最大弹性势能Epm=
kA2…③1 2
解得Epm=4J…④
根据机械能守恒定律可知小车的最大动能应等于弹簧的最大弹性势能
所以
kA2=1 2
Mvm2…⑤1 2
解得小车的最大速度vm=1m/s…⑥
(3)小物块b与小车a磁撞后,小车a的速度为vm,设此时小物块的速度为v1′,
设向右为正方向,由动量守恒定律有
mv1=mv′1+Mvm…⑦
解得v1′=-2m/s…⑧
接着小物块向左匀减速运动一直到停止,设位移是s1,所经历的时间为t1,
根据动能定理可知
-μmgs1=0-
mv1/2…⑨1 2
解得s1=1m…⑩
物块作匀减速运动时的加速度为
a=
=μg=2m/s2…(11)μmg 2m
t1=
=1s…(12)0- v /1 a
小车a振动的周期T=2π
≈1.26s…(13)M k
由于T>t1>
T,所以小车a在小物块b停止时在O点的左侧,并向右运动…(14)3 4
答:(1)小物块与小车磁撞前瞬间的速度是6m/s;
(2)小车做简谐运动过程中弹簧最大弹性势能是4J;小车的最大速度为1m/s;
(3)小物块最终停在距O点1m远处,当小物块刚停下时小车左端运动到O点的左侧,并向右运动.
