问题
问答题
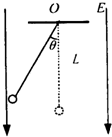
一个质量为m、带+q电量的小球,用长L的绝缘细线悬吊在竖直向下的场强为E的匀强电场中.如果将细线拉至与竖直方向成θ角,然后将小球无初速释放,如图所示.求小球运动到最低点时细线的拉力多大.
答案
设小球通过最低点时的速度为v,
根据动能定理:mgL(1-cosθ)+qEL(1-cosθ)=
mu2-0;1 2
解得v=
;(2g+
)L(1-cosθ)2qE m
根据牛顿第二定律:F=m
;v2 L
设线的拉力为T,则T-mg-qE=m
;v2 L
解得T=3mg+3qE-2(mg+qE)cosθ
答:小球运动到最低点时细线的拉力为3mg+3qE-2(mg+qE)cosθ.
