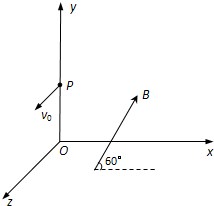
如图所示,在正交坐标系Oxyz的空间中,同时存在匀强电场和匀强磁场(x轴正方向水平向右,y轴正方向竖直向上).匀强磁场的方向与Oxy平面平行,且与x轴的夹角为60°.一质量为m、电荷量为+q的带电质点从y轴上的点P(0,h,0)沿平行于z轴正方向以速度v0射入场区,重力加速度为g.
(1)若质点恰好做匀速圆周运动,求电场强度的大小及方向;
(2)若质点恰沿v0方向做匀速直线运动,求电场强度的最小值Emin及方向;
(3)若电场为第(2)问所求的情况,撤去磁场,当带电质点P点射入时,求带电粒子运动到Oxz平面时的位置.

(1)由于质点做匀速圆周运动,所以质点受到的电场力、重力二力平衡,即:qE-mg=0
得:E=
向竖直向上 mg q
(2)如图甲所示,带电质点受重力mg、洛伦兹力f=qv0B、电场力F=qE的作用做匀速直线运动,
根据几何关系可知:当电场力方向与洛伦兹力方向垂直时,场强有最小值Emin,
所以电场强度Emin的方向与xOz的夹角为60°,即与磁感应强度B的方向相同.
根据牛顿运动定律:qEmin-mgsin60°=0 ①
f洛-mgcos60°=0 ②
由①②解得:Emin=
mg3 2q
(3)如乙所示,撤去磁场后,带电质点受到重力mg和电场力qEmin作用,
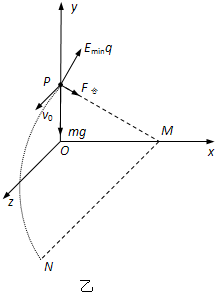
其合力与存在磁场时的洛伦兹力大小相等方向相反,即沿图中PM方向,合力与v0方向垂直.由②得 f洛=mgcos60°=
mg1 2
设经过时间t到达Oxz平面内的点N(x,y,z),由运动的合成和分解可得:
沿v0方向:z=v0t③
沿PM方向:PM=
at2④1 2
沿PM方向:PM=
=2h⑤h sin30°
联立③~⑤解得:x=
h3 z=2v0 2h g
所以.带电质点在N(
h,0,2v03
)的位置.2h g
答:(1)若质点恰好做匀速圆周运动,求电场强度的大小
及方向竖直向上;mg q
(2)若质点恰沿v0方向做匀速直线运动,则电场强度的最小值为
及方向与xOz的夹角为60°,即与磁感应强度B的方向相同;
mg3 2q
(3)若电场为第(2)问所求的情况,撤去磁场,当带电质点P点射入时,则带电粒子运动到Oxz平面时在N(
h,0,2v03
)的位置.2h g
