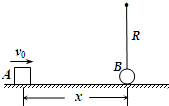
如图所示,长为R=0.6m的不可伸长的细绳一端固定在O点,另一端系着质量为m2=0.1kg的小球B,小球B刚好与水平面相接触.现使质量为m1=0.3kg物块A以v0=5m/s的初速度向B运动,A与水平面间的动摩擦因数μ=0.3,A、B间的初始距离x=1.5m.两物体碰撞后,A物块速度变为碰前瞬间速度的1/2,B小球能在竖直平面内做圆周运动.已知重力加速度g=10m/s2,两物体均可视为质点,试求:
(1)两物体碰撞前瞬间,A物块速度v1的大小;
(2)两物体碰撞后瞬间,B球速度v2的大小;
(3)B球运动到圆周最高点时细绳受到的拉力大小.
(1)与B碰撞之前,A做匀减速直线运动,
根据牛顿第二定律有:
a=
=F m
=μgμmg m
根据位移速度公式有:v12-v02=-2ax
解得v1=4m/s
(2)碰撞过程中,A、B系统动量守恒,有:
m1v1=m1
+m2v2v1 2
可得v2=6m/s
(3)小球B在摆至最高点过程中,机械能守恒,设到最高点时的速度为v3
m2v22=1 2
m2v32+m2g•2R1 2
在最高点:T-m2g=m2v32 R
解得T=1N
答:(1)两物体碰撞前瞬间,A物块速度v1的大小为4m/s;
(2)两物体碰撞后瞬间,B球速度v2的大小为6m/s;
(3)B球运动到圆周最高点时细绳受到的拉力大小为1N.
