问题
问答题
设f(x)在(0，+∞)内二阶可导，在[0，+∞)有连续的导数，且f"(x)＞0(x＞0)，求证：F(x)
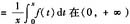是凹函数。
答案
参考答案：[分析与证明] 由题设条件可求得
[*]
下证[*]
由于[*]连续[*]
单调增加[*]
g(x)＞g(0)=0 (x＞0)[*]因此F(x)在(0，+∞)是凹函数。
搜题请搜索小程序“爱下问搜题”
设f(x)在(0，+∞)内二阶可导，在[0，+∞)有连续的导数，且f"(x)＞0(x＞0)，求证：F(x)
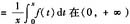是凹函数。
参考答案：[分析与证明] 由题设条件可求得
[*]
下证[*]
由于[*]连续[*]
单调增加[*]
g(x)＞g(0)=0 (x＞0)[*]因此F(x)在(0，+∞)是凹函数。