问题
问答题
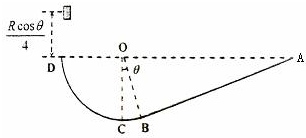
如图所示,竖直固定放置的粗糙斜面AB的下端与光滑的圆弧BCD的B点相切,圆弧轨道的半径为R,圆心O与A、D在同一水平面上,∠COB=θ,现有质量为m的小物体从距D点为
的地方无初速的释放,已知物体恰能从D点进入圆轨道.求:Rcosθ 4
(1)为使小物体不会从A点冲出斜面,小物体与斜面间的动摩擦因数至少为多少?
(2)若小物体与斜面间的动摩擦因数μ=
,则小物体在斜面上通过的总路程大小?sinθ 2cosθ
(3)小物体通过圆弧轨道最低点C时,对C的最大压力和最小压力各是多少?
答案
(1)为使小物体不会从A点冲出斜面,由动能定理得mg
-μmgcosθRcosθ 4
=0Rcosθ sinθ
解得动摩擦因数至少为:μ=sinθ 4cosθ
(2)分析运动过程可得,最终小物体将从B点开始做往复的运动,由动能定理得
mg(
+Rcosθ)-μmgScosθ=0Rcosθ 4
解得小物体在斜面上通过的总路程为:S=5Rcosθ 2sinθ
(3)由于小物体第一次通过最低点时速度最大,此时压力最大,由动能定理,得
mg(
+R)=Rcosθ 4
mv21 2
由牛顿第二定律,得
Nmax-mg=mv2 R
解得Nmax=3mg+
mgcosθ1 2
最终小物体将从B点开始做往复的运动,则有
mgR(1-cosθ)=
mv′21 2
Nmin-mg=mv′2 R
联立以上两式解得Nmin=mg(3-2cosθ)
由牛顿第三定律,得小物体通过圆弧轨道最低点C时对C的最大压力
Nmax′=3mg+
mgcosθ,1 2
最小压力Nmin′=mg(3-2cosθ).
