问题
问答题
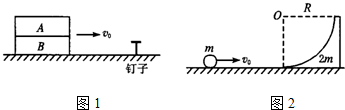
(1)如图1所示,A、B是两块完全相同的长木板,长度均为L,质量均为m.两板间动摩擦因数为μ,将两者边缘对齐叠放在光滑水平面上,并共同以某一水平速度v0向前运动.某时刻下面木板碰到水平面上固定的铁钉立即停止运动,为了使上面木板的前端不落在水平面上,求v0的大小范围.
(2)如图2所示,光滑水平面上有一带有
光滑圆弧轨道的滑块,其质量为2m,一质量为m的小球,以速度v0沿平面滑小轨道,并从轨道上某处又滑下,求小球上升到离水平面的最大高度.1 4
答案
(1)当上面木板相对下木板的位移s≤
时即不掉下. L 2
由牛顿第二定律得:A的加速度:a=
=-f m
=-μg;-μmg m
对A,由速度位移公式得:s=
,得-v02 2a
≤v02 2μg
,解得:所以v0≤L 2
;μgL
(2)设小球上升到最高点时,小球和滑块的水平速度为vx,
系统水平方向动量守恒.由动量守恒得mv0=(m+2m)vx,解得vx=
①,v0 3
小球上升到最高点时vy=0,系统机械能守恒,
由机械能守恒得:
mv02=1 2
(m+2m)vx2+mgh ②,1 2
解得h=
;v02 3g
答:(1)初速度v0≤
;μgL
(2)小球上升到离水平面的最大高度为
.v 20 3g
