如图所示,一根电阻为R=12Ω的电阻丝做成一个半径为r=1m的圆形导线框,竖直放置在水平匀强磁场中,线框平面与磁场方向垂直,磁感强度为B=0.2T,现有一根质量为m=0.1kg、电阻不计的导体棒,自圆形线框最高点静止起沿线框下落,在下落过程中始终与线框良好接触,已知下落距离为 r/2时,棒的速度大小为v1=
m/s,下落到经过圆心时棒的速度大小为v2=8 3
m/s,(取g=10m/s2)10 3
试求:
(1)下落距离为r/2时棒的加速度,
(2)从开始下落到经过圆心的过程中线框中产生的热量.
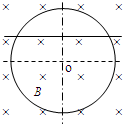
(1)下落距离为
时,闭合电路的总电阻:R=r 2
=
×R 3 2R 3 R
R ①2 9
导体棒切割磁感线的有效长度
L=
r ②3
此时感应电动势E=BLv1③
导体棒中电流:I=
④E R
导体棒受安培力:F=BIL⑤
方向竖直向上
由牛顿第二定律,mg-F=ma1⑥
由①②③④⑤⑥得a1=8.8 m/s2
(2)设从开始下落到经过圆心的过程中产生的热量为Q,重力势能的减小量转化为内能和动能的增加量;由能量守恒可知:
mgr=Q+
mv221 2
代入数值解得:Q=mgr-
mv2=0.44J1 2
答:(1)棒的加速度为8.8m/s2;(2)产生的热量为0.44J.
