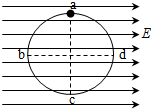
一半径为R的绝缘光滑圆环竖直放置在方向水平向右的、场强为E的匀强电场中,如图所示,环上a,c是竖直直径的两端,b,d是水平直径的两端,质量为m的带电小球套在圆环上,并可沿环无摩擦滑动,已知小球自a点由静止释放,沿abc运动到d点时的速度恰好为零,由此可知( )
A.小球在d点时的加速度为零
B.小球在d点时的电势能最大
C.小球在b点时的机械能最大
D.小球在b点时的动能最大
A、小球由a点释放,受到重力、向左的电场力和环的弹力作用,小球能沿abc运动到d点,即球由静到动再到静,故球在a点的加速度一定不为零,故A错误;
B、根据功能关系,电场力做负功,电势能增加;电场力向左,故运动到d点时克服电场力做的功最多,电势能增加的最多,故B正确;
C、根据功能关系,除重力外其余力做功等于机械能的增加量;小球受到重力、电场力和环的弹力作用,弹力沿径向,速度沿着切向,故弹力一直不做功,除重力外只有电场力做功,由于电场力水平向左,故运动到b点时,电场力做的功最多,机械能增量最大,故C正确;
D、根据动能定理,合力做的功等于动能的增加量;
从a到d过程,有:mg•R-qE•R=0
解得 qE=mg
即电场力与重力大小相等,故重力场和电场的复合场中的最低点在bc段圆弧的中点处,小球运动此处时动能最大,故D错误;
故选:BC.
