问题
解答题
(本题满分6分)已知关于x的方程k2x2+(2k-1)x+1=0有两个实数根x1、x2
(1)求k的取值范围;
(2)是否存在k的值,可以使得这两根的倒数和等于0?如果存在,请求出k,若不存在,请说明理由.
答案
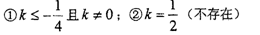
分析:
(1)根据方程由两个不相等的实数根,则有△≥0,可列出不等式,求出k的取值范围;
(2)根据一元二次方程根与系数的关系可求出x1+x2=-(2k-1)/ k2,x1x2=1/ k2,再根据题意可得1/ x1+1/ x2,把式子进行变形,进行代入可求出k的值。
解答:
(1)(2k-1)2-4k2×1≥0,
解得:k≤1/4,且k2≠0,
∴k≠0,
∴k≤-1/4且k≠0;
(2)不存在,
∵方程有两个的实数根,
∴x1+x2=-(2k-1)/ k2,x1x2=1/ k2,
∴1/ x1+1/ x2=(x2+x1)/ x1x2=[-(2k-1)/ k2]/(1/ k2)=-2k+1=0,
k=1/2,
∵k≤-1/4
且k≠0;
∴不存在。
点评:此题主要考查了根的判别式,以及一元二次方程根与系数的关系,关键是把握准计算公式:一元二次方程ax2+bx+c=0(a≠0)中:△=b2-4ac,x1+x2=-b/a,x1x2=c/a。
