某地区2000～2007年地区生产总值与税收收入资料如下表所示(单位

问题多项选择题

某地区2000～2007年地区生产总值与税收收入资料如下表所示(单位：亿元)：

年份	地区生产总值(X)	各项税收(Y)
2000	856	125
2001	970	135
2002	1130	143
2003	1407	164
2004	1599	192
2005	1770	200
2006	2404	213
2007	2404	238

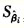根据上表资料求得： ∑X=12160 ∑Y=1440 ∑X²=20495678 ∑Y²=260072 ∑XY=2294560

=0.003813 ∑(Yi-

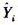)2=175.599356

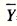=11383.90064

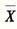=2012478 α取0.05，查表得：t_0.025(6)=2.447，F_0.05(1,6)=5.99 用Excel分析工具库中的“回归”模块得到下列结果：回归统计

R²	0.984809
修正的R²	0.982277
标准误差	5.409858
观测值	8

	df	SS	MS	F	Significance F
回归	1	11383.90064	11383.90064	388.97	1.10177E-06
残差	6	175.599356	29.266559
总计	7	11559.5

	系数	标准误差	t统计量	P-value
截距	61.92964	6.103886	10.15	5.33238E-05
变量(X)	0.075211	0.003813	19.72	1.10177E-06

请根据上述资料从下列备选答案中选出正确答案。(提示：考生可以根据本题给出的中间结果进行计算和分析，也可以根据Excel的输出结果直接进行分析。)

根据题中所给资料，指出下列正确的说法是（）。

A．地区生产总值与税收收入的相关系数r=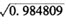=0.992375

B．R²=0.984809表示在Y的总变差中，有98.4809%可以由解释变量X做出解释

C．Y_i=61.92964+0.075211X_i，回归系数表示地区生产总值每增加1亿元，税收收入增加0.075211亿元

D．Y_i=61.92964+0.075211X_i，回归系数表示地区生产总值每增加1亿元，税收收入平均增加0.075211亿元

答案

参考答案：A, B, D

解析：

[答案] ABD

已知R²=0.984809，那么相关系数r=

=0.992375，并且R²=0.984809表示在Y的总变差中，有98.4809%可以由解释变量X(或回归方程)做出解释；已知斜率为0.075211，截距为61.92964，那么回归方程为Y=61.92964+0.075211X_i，其中回归系数(斜率)表示地区生产总值每增加1亿元，税收收入平均增加0.075211亿元。