问题
填空题
设函数f(x)在(0，+∞)上连续且对任意正值a与b，积分
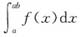的值与a无关，且f(1)=1．则f(x)=______．
答案
参考答案：[*]．
解析：
[分析]： 由[*]与a无关，所以[*]，即
f(ab)b-f(a)≡O．
上式对任意a成立，所以命a=1亦应成立，有f(b)b-f(1)=0，[*]，即有f[*]．可以验算，[*]，与a无关．
搜题请搜索小程序“爱下问搜题”
设函数f(x)在(0，+∞)上连续且对任意正值a与b，积分
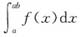的值与a无关，且f(1)=1．则f(x)=______．
参考答案：[*]．
解析：
[分析]： 由[*]与a无关，所以[*]，即
f(ab)b-f(a)≡O．
上式对任意a成立，所以命a=1亦应成立，有f(b)b-f(1)=0，[*]，即有f[*]．可以验算，[*]，与a无关．