已知函数f(x)对任意实数x,y恒有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0,又f(1)=-2.
(1)判断f(x)的奇偶性;
(2)求证:f(x)是R上的减函数;
(3)求f(x)在区间[-3,3]上的值域;
(4)若∀x∈R,不等式f(ax2)-2f(x)<f(x)+4恒成立,求a的取值范围.
(1)奇函数
(2)见解析
(3)[-6,6]
(4)(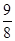 ,+∞)
,+∞)
解:(1)取x=y=0,则f(0+0)=2f(0),∴f(0)=0.
取y=-x,则f(x-x)=f(x)+f(-x),
∴f(-x)=-f(x)对任意x∈R恒成立,∴f(x)为奇函数.
(2)证明: 任取x1,x2∈(-∞,+∞),且x1<x2,则x2-x1>0,f(x2)+f(-x1)=f(x2-x1)<0,
∴f(x2)<-f(-x1),又f(x)为奇函数,
∴f(x1)>f(x2).
∴f(x)是R上的减函数.
(3)由(2)知f(x)在R上为减函数,
∴对任意x∈[-3,3],恒有f(3)≤f(x)≤f(-3),
∵f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=-2×3=-6,
∴f(-3)=-f(3)=6,f(x)在[-3,3]上的值域为[-6,6].
(4)f(x)为奇函数,整理原式得f(ax2)+f(-2x)<f(x)+f(-2),
则f(ax2-2x)<f(x-2),
∵f(x)在(-∞,+∞)上是减函数,∴ax2-2x>x-2,
当a=0时,-2x>x-2在R上不是恒成立,与题意矛盾;
当a>0时,ax2-2x-x+2>0,要使不等式恒成立,则Δ=9-8a<0,即a>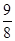 ;
;
当a<0时,ax2-3x+2>0在R上不是恒成立,不合题意.
综上所述,a的取值范围为(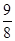 ,+∞).
,+∞).
