问题
问答题
当两个证券资产之间的相关系数为-1时，推导出由这两个证券构成的组合在
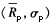坐标系中所有可能位置的表达式。
答案
参考答案：
解析：当两个证券资产之间的相关系数为-1时，推导出由这两个证券构成的组合在
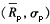坐标系中所有可能位置的表达式。
[解] 设两个证券资产为A、B，它们的期望收益率分别为
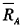和
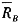，方差分别为σA和σB，并设资产组合中证券A的比例为引则组合的期望收益率和方差分别为：
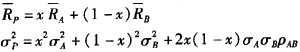
由ρAB=-1，所以：
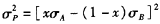
当xσA-(1-x)σB＞0即
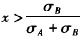时，有：
σP=xσA-(1-x)σB
进一步解得
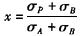
代入
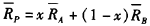即可得到：
当xσA-(1-x)σB＜0即
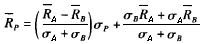时，同样可以得到：
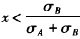
综上所述，由两个证券A、B构成的组合在
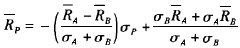坐标系中所有可能位置的表达式为：
