问题
问答题
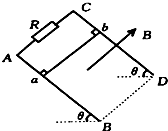
如图所示,AB、CD是两根足够长的光滑固定平行金属导轨,两导轨间的距离为L,导轨平面与水平面的夹角为θ,在整个导轨平面内都有垂直于导轨平面斜向上方的匀强磁场,磁感应强度为B,在导轨的 AC端连接一个阻值为 R的电阻,一根质量为m、垂直于导轨放置的金属棒ab,从静止开始沿导轨下滑.(导轨和金属棒的电阻不计)
(1)求导体下滑过程中速度为v时加速度是多少?
(2)求导体ab下滑的最大速度vm;
(3)若金属棒到达最大速度时沿斜面下滑的距离是S,求该过程中R上产生的热量.
答案
(1)经分析知,金属棒先沿斜面向下做加速度逐渐减小的加速运动,
由牛顿第二定律得 mgsinθ-BIL=ma
又I=BLv R
解得:a=gsinθ-B2L2v R
(2)当加速度减小到0时,达到最大速度,此时:
mgsinθ=BIL
又I=BLvm R
解得 vm=mgRsinθ B2L2
(3)由能量转化和守恒定律知,金属棒减少的机械能转化为回路中的焦耳热,即△Q=mgSsinθ-
mv21 2
答:
(1)导体下滑过程中速度为v时加速度是gsinθ-B2L2v R
(2)导体ab下滑的最大速度vm为
;mgRsinθ B2L2
(3)若金属棒到达最大速度时沿斜面下滑的距离是S,该过程中R上产生的热量为mgSsinθ-
mv2.1 2
