问题
问答题
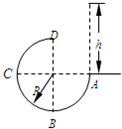
如图所示，固定在竖直平面内的光滑圆弧形轨道ABCD，半径为R，其A、C点与圆心等高，D点为轨道最高点．现使小球自A点正上方某处由静止释放，从A点进入圆轨道运动，小球恰好能通过D点．已知当地的重力加速度为g，不计空气阻力，试求：
（1）小球释放点到A点的高度h；
（2）小球通过C点时轨道对它的支持力N．
答案
（1）设小球的质量为m，通过C点和D点时的速度分别为vC和vD，由于小球恰好能通过D点，说明在D点轨道对小球的支持力为零，
根据牛顿第二定律可知mg=mvD2 R
根据机械能守恒定律可知mg(h-R)=
mvD2 1 2
联立解得h=
R3 2
（2）根据机械能守恒定律可知mgh=
mvC21 2
根据牛顿第二定律可知N=mvC2 R
联立解得小球通过C点时轨道对它的支持力 N=3mg．
答：（1）小球释放点到A点的高度h=
R．3 2
（2）小球通过C点时轨道对它的支持力为3mg．
丙(g)+丁(g)，△H=-akJ/mol（a>0） 下列说法正确的是（ ）