如图所示，质量为m=1kg的滑块，在水平力作用下静止在倾角为θ=30

问题问答题

如图所示，质量为m=1kg的滑块，在水平力作用下静止在倾角为θ=30°在光滑斜面上，斜面的末端B与水平传送带相接（物块经过此位置滑上皮带时无能量损失），传送带的运行速度为v₀=3m/s，长为L=1.4m；今将水平力撤去，当滑块滑到传送带右端C时，恰好与传送带速度相同．滑块与传送带间的动摩擦因数为μ=0.25．g=10m/s²

求：

（1）水平作用力F大小．

（2）滑块下滑的高度．

（3）若滑块进入传送带速度大于3m/s，滑块在传送带上滑行的整个过程中产生的热量．

答案

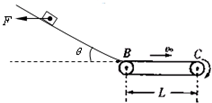
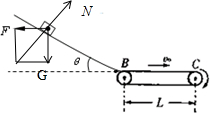
（1）滑块受到水平推力F、重力mg和支持力N处于平衡，如图所示，水平推力F=mgtanθ

（2）设滑块从高为h处上滑，到达斜面底端速度为v，

下滑过程机械能守恒：

mgh=

mv²

解得：v=

2gh

；

若滑块冲上传送带的速度小于传送带速度，则滑块在带上由于受到向右的滑动摩擦力而做匀加速运动，根据动能定理有：

μmgL=

mv₀²-

mv²

联立解得：h=

-μL=0.1m；

若滑块冲上传送带时的速度大于传送带的速度，则滑块由于受天向左的滑动摩擦力而做匀速运动，根据动能定理：

-μmgL=

mv₀²-

mv²

解得：h=

+μL=0.8m

（3）设滑块在传送带上运动的时间为t，则t时间内传送带的位移：

s=v₀t

由机械能守恒可知：mgh=

mv^{2
解得：v=
2gh
对滑块由运动学公式知：
v₀=v-at
联立解得：s=v₀
v-v0
a
滑块相对传送带滑动的位移△s=L-s
相对滑动生成的热量Q=μmg△s=0.5J．
答：（1）水平作用力为
10
3
3
N；（2）滑块下滑的高度可能为0.1m或0.8m；（3）相对滑块生成的热量为0.5J．}