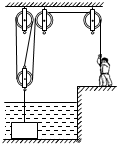
如图所示,质量为70kg的工人站在岸边通过一滑轮组打捞一块沉没在水池底部的石材,该滑轮组中动滑轮质量为5kg.当工人用120N的力拉滑轮组的绳端时,石材仍沉在水底不动.工人继续增大拉力将石材拉起,在整个提升过程中,石材始终以0.2m/s的速度匀速上升.在石材还没有露出水面之前滑轮组的机械效率为η1,当石材完全露出水面之后滑轮组的机械效率为η2,且η1:η2=63:65.绳重及滑轮的摩擦均可忽略不计,石材的密度
ρ石=2.5×103kg/m3,取g=10N/kg,求:
(1)当人用120N的力拉绳端时,岸边地面对人的支持力为多大;
(2)在石材脱离水池底部至完全露出水面的过程中,地面对人的支持力的最大值与最小值之比;
(3)当石材露出水面之前,人拉绳子的功率;
(4)此人用这个滑轮组提升重物的最大机械效率.
工人的重力:
G人=m人g=70kg×10N/kg=700N,
动滑轮的重力:
G动=m动g=5kg×10N/kg=50N,
未露出水面滑轮组的机械效率:
η=
=W有 W总
=(G石-F浮)h (G石-F浮+G动)h
,G石-F浮 G石-F浮+G动
露出水面后滑轮组的机械效率:
η=
=W有 W总
=G石h (G石+G动)h
,G石 G石+G动
∵η1:η2=63:65,
即
:ρ石Vg-ρ水Vg ρ石Vg-ρ水Vg+50N
=63:65,ρ石Vg ρ石Vg+50N
将石块的密度和水的密度代入求得:
V石=0.04m3,
石块的重力:
G石=m石g=ρ石V石g=2.5×103kg/m3×10N/kg×0.04m3=1000N,
(1)地面对人的支持力:
F=G人-F拉=700N-120N=580N;
(2)石材在水中,受到水的浮力,此时人的拉力最小,地面对人的支持力最大,
石材受到的浮力:
F浮=ρ水V排g=1×103kg/m3×10N/kg×0.04m3=400N,
F拉1=
(G石+G动-F浮)=1 3
(1000N+50N-400N)=1 3
N,650 3
地面的支持力:
F支1=G人-F拉1=700N-
N=650 3
N;1450 3
石材离开水面,此时人的拉力最大,地面对人的支持力最小,
F拉2=
(G石+G动)=1 3
(1000N+50N)=350N,1 3
地面的支持力:
F支2=G人-F拉2=700N-350N=350N;
F支1:F支2=
N:350N=29:21;1450 3
(3)当石材露出水面之前,F拉1=
(G石+G动-F浮)=1 3
(1000N+50N-400N)=1 3
N,650 3
v=3×0.2m/s=0.6m/s
人拉绳子的功率:
P=F拉1v=
N×0.6m/s=130W;650 3
(4)重物露出水面后,滑轮组受到的向下的拉力最大,为F=G人=700N,
∵绳重及滑轮的摩擦均可忽略不计,
∴F=
(G物+G动),1 3
∴G物=3F-G动=3×700N-50N=2050N,
η=
=W有 W总
=Gh Fs
=Gh F•3h
=G 3F
≈97.6%.2050 3×700
答:(1)当人用120N的力拉绳端时,岸边地面对人的支持力为580N;
(2)在石材脱离水池底部至完全露出水面的过程中,地面对人的支持力的最大值与最小值之比为29:21;
(3)当石材露出水面之前,人拉绳子的功率为130W;
(4)此人用这个滑轮组提升重物的最大机械效率为97.6%.
