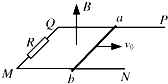
如图所示,光滑的U型金属导轨PQMN水平地固定在竖直向上的匀强磁场中.磁感应强度为B,导轨的宽度为L,其长度足够长,QM之间接有一个阻值为R的电阻,其余部分电阻不计.一质量为m,电阻也为R的金属棒ab,恰能放在导轨之上并与导轨接触良好.当给棒施加一个水平向右的冲量,棒就沿轨道以初速度v0开始向右滑行.求:
(1)开始运动时,棒中的瞬间电流i和棒两端的瞬间电压u分别为多大?
(2)当棒的速度由v0减小到
v0的过程中,棒中产生的焦耳热Q是多少?棒向右滑行的位移x有多大?1 10
(1)开始运动时,棒中的感应电动势:
e=Lv0B
棒中的瞬时电流:i=
=e 2R BLv0 2R
棒两端的瞬时电压:u=
e=R R+R
Lv0B1 2
(2)由能量转化与守恒定律知,全电路在此过程中产生的焦耳热:
Q总=
mv02-1 2
m(1 2
v0)2=1 10
mv02 99 200
∴棒中产生的焦耳热为:Q=
Q总=1 2
mv02 99 400
令:△t表示棒在减速滑行时某个无限短的时间间隔,则在这一瞬时,结合安培力
和瞬时加速度的极限思想,应用牛二律有:
iLB=m△v △t
结合电磁感应定律和瞬时速度的极限思想,应用全电路欧姆定律有:
i•2R=LBv=LB△x △t
所以:mLB△v=LB•2R△x,即:△x∝△v
所以对于全过程,上述正比例关系仍成立
所以对于全过程(△v=
v0),得:9 10
△x=x=9 10
v0Rm L2B2
答:(1)开始运动时,棒中的瞬间电流i=
和棒两端的瞬间电压u=BLv0 2R
Lv0B;1 2
(2)当棒的速度由v0减小到
v0的过程中,棒中产生的焦耳热Q=1 10
mv02;棒向右滑行的位移x=99 400 9 10
v0.Rm L2B2
