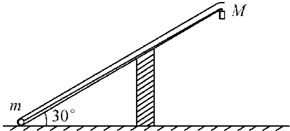
如图所示,长为L、内壁光滑的直管与水平地面成30°角固定位置.将一质量为m的小球固定在管底,用一轻质光滑细线将小球与质量为M=3m的小物块相连,小物块悬挂于管口.现将小球释放,一段时间后,小物块落地静止不动,小球继续向上运动,通过管口的转向装置后做平抛运动,小球在转向过程中速率不变(重力加速度为g).
求:(1)小物块下落过程中的加速度大小;
(2)小球从管口抛出时的速度大小;
(3)小球在做平抛过程中的水平位移.
(1)设细线中的张力为T,根据牛顿第二定律:
Mg-T=Ma
T-mgsin30°=ma
且M=3m
解得a=
g 5 8
答:小物块下落过程中的加速度大小为
g. 5 8
(2)设M落地时的速度大小为v,m射出管口时速度大小为v0,M落地后m的加速度为a0.根据牛顿第二定律有:
-mgsin30°=ma0
解得a0=-gsin30°=-
g1 2
又由匀变速直线运动,
v2=2aLsin30°,
v02-v2=2a0L(1-sin30°)
解得v0=gl 8
答:小球从管口抛出时的速度大小为
.gl 8
(3)小球做平抛运动有:
x=v0t
Lsin30°=
gt2 1 2
解得水平位移x=
L2 4
答:小球在做平抛过程中的水平位移为=
L.2 4
