问题
问答题
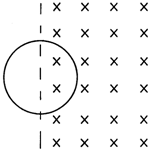
一有界匀强磁场区域如图所示,质量为m,电阻为R,半径为r的圆形线圈一半在磁场内,一半在磁场外,t=0时磁感应强度为B,以后均匀减小直至零,磁感应强度的变化率
为一常数k,线圈中产生感应电流,在磁场力作用下运动,不考虑重力影响.求△B △t
(1)t=0时刻线圈的加速度.
(2)线圈最后做匀速直线运动时回路中的电功率.
答案
(1)由法拉第电磁感应定律得:
E=
=S•△Φ △t △B △t
又S=
πr2,1 2
=k △B △t
由闭合电电路的欧姆定律
I=E R
由安培力公式:
F=BI•2r
由牛顿第二定律
a=F m
联立以上各式得:a=
.Bπkr3 mR
(2)线圈做匀速直线运动,有三种可能
(a)线圈没有全部进入磁场,磁场就消失,所以以后没有感应电流,回路电功率P=0
(b)线圈全部进入磁场,磁场没有消失,尽管有感应电流,但所受合力为零,同样做匀速直线运动,电功率P=E2 R
结合(1)中E的求法可知E′=k•πr2解得P=π2r4k2 R
(c)在上面(b)的前提下,等到磁场消失后,电功率P=0.
答:(1)t=0时刻线圈的加速度a=
.Bπkr3 mR
(2)线圈最后做匀速直线运动时回路中的电功率可能为0或
.π2r4k2 R
