问题
问答题
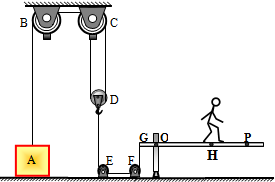
如图所示小星沿杠杆GP水平向右匀速运动,通过对杠杆GP施加竖直向下的压力来提升物体A.其中B、C、E、F都是定滑轮,D是动滑轮,杠杆GP可绕O点在竖直平面内转动.正立方体A的边长为40cm,密度为5×103kg/m3.杠杆GP和细绳的质量均忽略不计,OG为10cm.当小星运动到H点,物体A对水平地面的压强为0Pa.此时通过细绳对动滑轮D的向下拉力FD=6000N.忽略细绳与滑轮的摩擦.g取10N/kg.求:
(1)物体A的重力;
(2)动滑轮D的重力;
(3)若人的质量为40Kg,则OH的长度是多少?
答案
(1)物体A的体积:
VA=(0.4m)3=0.064m3,
物体A的重力:
GA=mAg=ρAGVA=5×103kg/m3×10N/kg×0.064m3=3200N;
(2)以物体A为研究对象,受力分析如图1所示.
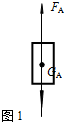
FA=GA=3200N,
以动滑轮为研究对象,受力分析如图2所示.
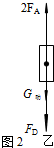
2FA=FD+G动;
2×3200N=6000N+G动,
解得:G动=400N;
(3)由于人对杠杆的压力等于人的重力,G人=m人g=40kg×10N/kg=400N,
对杠杆进行受力分析如图3所示:
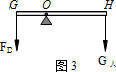
根据杠杆平衡条件可得:
FD×OG=G人×0H,
6000N×0.1m=400N×0H,
0H=1.5m.
答:(1)物体A的重力为3200N;
(2)动滑轮D的重力为400N;
(3)若人的质量为40Kg,则OH的长度是1.5m.
