问题
问答题
如图所示,传送带与水平面之间的夹角为θ=30°,其上A、B两点间的距离为S=5m,传送带在电动机的带动下以v=2m/s的速度匀速运动.现将一质量为m=10Kg的小物体(可视为质点)轻放在传送带的A点,小物体与传送带之间的动摩擦因数μ=
,在传送带将小物体从A点传送到B点的过程中,求:(g取10m/s2)3 2
(1)小物体做加速运动阶段的位移S1;
(2)小物体与传送带之间的摩擦力做功产生的热量Q;
(3)传送带对小物体做的功W.

答案
(1)如图,对小物体进行受力分析有:
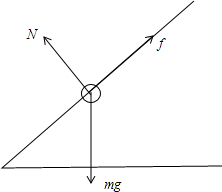
由图分析知:N=mgcosθ
f=μN=μmgcosθ
令小物体加速后能达到传送带的运动速度,则由动能定理得:
(μmgcosθ-mgsinθ)S1=
mv2-01 2
代入数值得S1=0.8m
∵S1<S
∴加速阶段小物体的位移S1=0.8m
(2)小物体在加速阶段做匀加速运动,令运动时间为t,则小物体运动的位移为
S1=
t=0.8m0+v 2
在这段时间内传送带运动的位移
S2=vt=1.6m
所以摩擦产生的热量等于摩擦力乘以两物体间的相对距离
即Q=μmgcosθ(S2-S1)=
×10×10×cos30°(1.6-0.8)J=60J3 2
(3)根据功能关系,传送带对小物体做的功等于小物体机械能的增量
即:
W=
mv2+mgSsinθ=1 2
×10×22+10×10×5×sin30°J=270J1 2
答:(1)小物体做加速运动阶段的位移S1=0.8m;
(2)小物体与传送带之间的摩擦力做功产生的热量Q=60J;
(3)传送带对小物体做的功W=270J.
