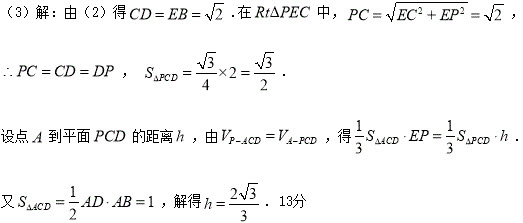问题
问答题
如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱
，底面ABCD为直角梯形，其中BC∥AD，AB⊥AD，AD=2AB=2BC=2，点0为AD中点。
(1)求证：PE平面ABCD；
(2)求异面直线PB与CD所成角的余弦值；
(3)求点A到平面PCD的距离。
答案
参考答案：
因为在APAD中，PA=PD，点O为AD中点，
所以PO⊥AD。
又因为侧面PAD⊥底面ABCD，平面PAD∩平面ABCD=AD，PO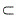
平面PAD，
所以PO⊥平面ABCD。
(2)连接BO，
在直角梯形ABCD中，BC∥AD，AD=2AB=2BC，
则OD∥BC，且OD=BC，
所以四边形OBCD是平行四边形，
所以OB∥DC。
由(1)知PO⊥OB，∠PBO为锐角，
所以∠PBO是异面直线PB与CD所成的角。
因为AD=2AB=2BC=2，
且在Rt△AOB中，AB=1，AO=1，
所以OB=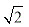
在Rt△POA中，因为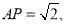
AO=1，
所以OP=1。
在Rt△PBO中，
