问题
问答题
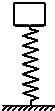
如图所示,质量m的物体在竖直弹簧上做简谐运动,当振幅为A时,木块对弹簧压力的最大值为木块重力的1.5倍,求:
(1)木块对弹簧压力的最小值为多少?
(2)欲使木块不脱离弹簧,其振幅不能超过多少?
答案
(1)因为木块在竖直方向上做简谐运动,依题意木块在最低点时对弹簧的压力最大,在最高点对弹簧的压力最小.
在最低点根据牛顿第二定律有FN-mg=ma,代入数据解得a=0.5 g.
由最高点和最低点相对平衡位置对称,加速度大小等值反向,所以最高点的加速度大小为a′=0.5 g,在最高点根据牛顿第二定律有mg-FN′=ma′,
故FN′=mg-ma′=0.5 mg.
答:木块对弹簧压力的最小值为0.5mg.
(2)要使木块不脱离弹簧,设其振幅不能超过A′,此时木块振到最高点恰在弹簧原长处,此时的最大加速度为g,由a=-
x知,当振幅为A时,在最低点有0.5 g=-k m
A;k m
当振幅为A′时,在最高点有g=-
A′,由此可得A′=2A.k m
答:欲使木块不脱离弹簧,其振幅不能超过2A.
