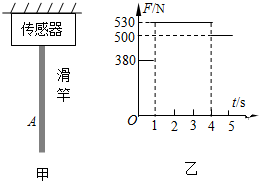
如图甲为消防员训练时的一种器械,一质量不计的竖直滑竿,滑竿上端固定,下端悬空.为了研究消防员沿竿的下滑情况,在竿的顶部装有一拉力传感器,可显示竿的顶端所受拉力的大小.现有一质量m=50kg的消防员(可视为质点)从滑竿顶端由静止开始滑下,4s末滑到竿A点时开始匀速下滑.以消防员开始下滑时刻为计时起点,传感器显示的拉力随时间变化情况如图乙所示,g取10m/s2.求:
(1)该消防员下滑过程中的最大速度.
(2)A点到滑竿顶端的长度.
(1)由题意分析知:传感器显示的拉力大小为消防员所受竿的摩擦力的大小.
由F-t 知:消防员先加速下滑1s末开始减速下滑,4s末后匀速下滑,所以最大速度出现在1s末:
0~1s,由牛顿第二定律:F合=ma
所以:mg-f=ma1
即:500-380=50a1;得a1=2.4m/s2.
1s末的速度:v1=at=2.4×1m/s=2.4m/s.
(2)0~1s的位移:s1=
at2=1 2
×2.4×12=1.2m1 2
1~4s的加速度:
a2=
=F合 m
=mg-f m
=-0.6m/s2.500-530 50
1~4的位移:
s2=v0t+
at2=2.4×3+1 2
×(-0.6)×32=4.5m1 2
A点到滑杆顶端的长度:
h=s1+s2=1.2+4.5m=5.7m.
答:(1)该消防员下滑过程中的最大速度为2.4m/s.
(2)A点到滑竿顶端的长度为5.7m.
