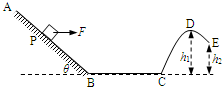
如图,AB为粗糙的长直斜面,动摩擦因数μ=0.4,与水平方向的夹角θ=37°,BC为光滑水平面,CDE为光滑曲面,B、C两接口处均光滑连接.D、E两点离水平地面的高度分别为h1=8.64m,h2=4m.一质量m=0.20kg的滑块由斜面上某一点P从静止开始下滑,在斜面上始终受一水平向右恒力F=1N的作用,到达B点时立即撤去拉力F,从P点到达C点共经历t=3s.已知PB与BC长度之和为32m.求:(sin37°=0.6,cos37°=0.8,g=10m/s2)
(1)滑块沿AB段运动时加速度a和所用时间t1;
(2)若水平向右恒力F大小可调,则恒力F在何范围内可使滑块沿PB、BC运动越过曲面落地.某同学对第二问的解答如下:若要使滑块越过曲面落地,则离开曲面E点时的速度至少为0.从P点至E点列出动能定理.即可求得所需的最小恒力.请判断该同学的解答是否正确,并说明理由,若该同学解答错误则求出正确的恒力范围.
(1)由牛顿第二定律Fcosθ+mgsinθ-μN=ma ①
由垂直斜面方向受力平衡可得N=mgcosθ-Fsinθ ②
联立①②可得加速度a=8m/s2
S=S1+S2=
a1t12+a1t1(t-t1)1 2
得t1=2s
(2)该同学回答错误.
错误1:至少滑到D点速度为0才可以越过曲面落地.
错误2:在斜面上力F不能过大,否则物块将离开斜面运动.
从P至D动能定理WG+WF+Wf=△EKmg(s1sinθ-h1)+F1s1cosθ-μ(mgcosθ-F1sinθ)s1=0
得F1=0.5N
F2sinθ=mgcosθ
得F2=2.67N
所以恒力F的范围应该为F1<F≤F2
即0.5N<F≤2.67N
答:(1)滑块沿AB段运动时加速度为8m/s2,所用时间为2s.
(2)恒力的范围为0.5N<F≤2.67N.
