问题
单项选择题
下列结论正确的是
(A) 若x0是函数f(x)的极小值点，则在x0的某一邻域内，f(x)在x0的左侧单调减少，而在右侧单调增加．
(B) 若x0为函数f(x)的极值点，则必有f’(x0)=0．
(C) 若偶函数f(x)具有连续的二阶导数，且f"(0)＞0，则点x=0一定是f(x)的极小值点．
(D) 若f’(x0)=0，但f"(x0)不存在，则点x=x0不可能为函数f(x)的极值点．
答案
参考答案：C
解析： 对于(A)：例如函数
显然f(0)=0为极小值，且
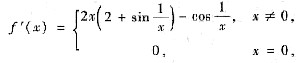
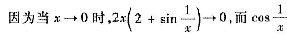却在-1与+l之间振荡，因而函数f(x)在点x=0左右两则都不是单调的．故(A)不正确．
[评注] 该命题说明两侧单调只是判别函数取得极值的充分务件，但非必要条件．
对于(B)：显然不对．正确的命题是：若x0是f(x)的极值点，且f’(x0)存在，则必定有f’(x0)=0成立．
[评注] 该命题说明，连续函数取得极值的必要条件为该点是驻点或不可导点．
对于(C)：对等式f(-x)=f(x)两端求导，并令x=0，得f(0)=0．又因为f"(0)＞0，所以x=0为f(x)的极小值点．故(C)正确．
对于(D)：例如函数
易知f’(0)=0，f"(0)不存在，而f(x)在点x=0处取得极小值．故(D)不正确．
[评注] f’(x0)=0，f"(x0)≠0，只是函数f(x)在点x=x0处取得极值的充分条件，并非必要条件．
综上分析，应选(C)．