问题
问答题
确定方程
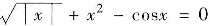 在(-∞,+∞)内根的个数,并证明之.
在(-∞,+∞)内根的个数,并证明之.
答案
参考答案:令
 ,则f(x)是偶函数且f(0)=-1<0,从而只需讨论f(x)在(0,+∞)内零点的个数即可.
,则f(x)是偶函数且f(0)=-1<0,从而只需讨论f(x)在(0,+∞)内零点的个数即可.
在(0,+∞)内,
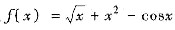 ,显然x≥1时f(x)≥1,所以只需在(0,1)内考察
,显然x≥1时f(x)≥1,所以只需在(0,1)内考察
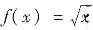 +x2-cosx零点的个数.由于
+x2-cosx零点的个数.由于
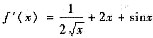 在(0,1)内大于零,所以在(0,1)内f(x)=
在(0,1)内大于零,所以在(0,1)内f(x)=
 单调增加,又因为f(0)=-1,f(1)>1,由零点定理知
单调增加,又因为f(0)=-1,f(1)>1,由零点定理知
 在(0,1)内有且只有一个零点.综上知函数
在(0,1)内有且只有一个零点.综上知函数
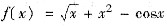 在(0,+∞)内有唯一的一个零点.
在(0,+∞)内有唯一的一个零点.
综合可知方程
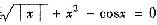 在(-∞,+∞)内恰有两个实根.
在(-∞,+∞)内恰有两个实根.
解析: 确定或讨论方程f(x)=0实根的个数或函数f(x)零点个数的解题思路为:先求函数f(x)的单调区间;在每一个单调区间上使用广义零点定理判定函数f(x)在该区间上是否有零点,将所有单调区间都讨论完,即可得到结论.
