参考答案：[证] 令f(x)=e^x+e^-x+2cosx-5，则f(x)是(-∞，+∞)上的偶函数，且f(0)≠0．所以方程e^x+e^-x+2cosx=5恰有两个实根的充要条件是函数
f(x)=e^x+e^-x+2cosx-5
在区间(0，+∞)内有唯一零点．
由于

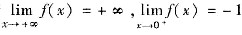，所以根据广义零点定理可得，函数f(x)在区间(0，+∞)内至少有一个零点．
又因为f’(x)=e^x-e^-x-2sinx，f"(x)=e^x+e^-x-2cosx≥0，所以f(x)单调增加，而f’(0)=0，所以在区间(0，+∞)内f’(x)＞0，从而f(x)在区间(0，+∞)内单调增加，故f(x)在区间(0，+∞)内最多有一个零点．
综上函数f(x)=e^x+e^-x+2cosx-5在区间(0，+∞)内有唯一零点，所以方程e^x+e^-x+2cosx=5恰有两个实根．