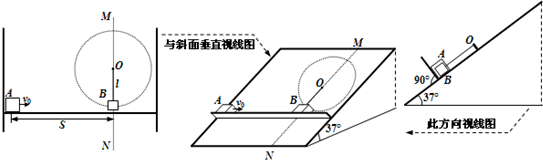
如图所示,倾角为37°的足够大斜面以直线MN为界由两部分组成,MN垂直于斜面水平底边PQ且其左边光滑右边粗糙,斜面上固定一个既垂直于斜面又垂直于MN的粗糙挡板.质量为m1=3kg的小物块A置于挡板与斜面间,A与挡板间的动摩擦因数为μ1=0.1.质量为m2=1kg的小物块B用不可伸长的细线悬挂在界线MN上的O点,细线长为l=0.5m,此时,细线恰好处于伸直状态.A、B可视为质点且与斜面粗糙部分的动摩擦因数均为μ2=0.3,它们的水平距离S=7.5m.现A以水平初速v0=5m/s向右滑动并恰能与B发生弹性正撞.g=10m/s2.求:
(1)A碰撞前向右滑动时受到的摩擦力;
(2)碰后A滑行的位移;
(3)B沿斜面做圆周运动到最高点的速度.

(1)分析物块A的受力得:f=μ1m1gsin37°=0.1×3×10×0.6=1.8(N)
(2)设A运动至与B相碰前速度为 v1,由动能定理得:
-μ1m1gsin370•s=
m11 2
-v 21
m11 2 v 20
解得:v1=4m/s
A和B发生弹性正碰,由动量守恒和能量守恒得:
m1v1=m1v'1+m2v2
m11 2
=v 21
m1v1 2
+′ 21
m21 2 v 22
解得:v'1=2m/s v2=6m/s
设A滑行的位移为s1,由动能定理得:
-(μ2m1gcos37°+μ1m1gsin37°)s1=0-
m1v1 2 ′ 21
解得:s1=
m≈0.67m2 3
(3)设B做圆周运动到最高点的速度为v3,
由动能定理得:-μ2m2gcos37°πl-m2gsin37°•2l=
m21 2
-v 23
m21 2 v 22
代入解得 v3≈4.1m/s
答:
(1)A碰撞前向右滑动时受到的摩擦力1.8N;
(2)碰后A滑行的位移为0.67m;
(3)B沿斜面做圆周运动到最高点的速度为4.1m/s.
