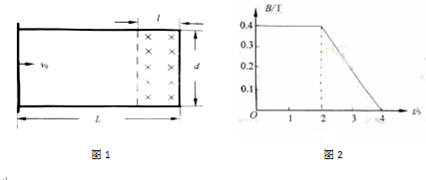
如图1所示,在水平面上固定有长为L=2m、宽为d=1m的金属“U”型导轨,在“U”型导轨右侧l=0.5m范围内存在垂直纸面向里的匀强磁场,其磁感应强度随时间变化的规律如图2所示.在t=0时刻,质量为m=0.1kg的导体棒以v0=1m/s的初速度从导轨的左端开始向右运动,导体棒与导轨之间的动摩擦因数为μ=0.1,导轨与导体棒单位长度的电阻均为λ=0.2Ω/m,不计导体棒与导轨之间的接触电阻及地球磁场的影响.求:
(1)导体棒从t=0时刻开始向右运动直至末速为零所需的时间;
(2)导体棒从t=0时刻开始向右运动直至末速为零时离左端的位置;
(3)4s内回路中电流的大小,并判断电流方向;
(4)4s内回路产生的焦耳热.
(1)根据牛顿第二定律得:
-μmg=ma,a=-μg=-1m/s2,
导体棒从t=0时刻开始向右运动直至末速为零所需的时间为 t=
=1s,v0 a
(2)此过程导体棒通过的位移为 x=v0t+
at2=0.5m<L-l,说明导体棒还没有进入磁场.1 2
(3)前2秒内无电流,后2秒内,由楞次定律判断得知,电流方向为顺时针方向.
由图知,
=△B △t
T/s=0.2T/s0.4 2
感应电动势为E=
=△Φ △t
•ld=0.2×0.5×1V=0.1V△B △t
感应电流为I=
=E 2λ(d+L-s)
A=0.1A,0.1 2×0.2×(1+2-0.5)
(4)4s内回路产生的焦耳热为 Q=IEt2=0.02J.
答:
(1)导体棒从t=0时刻开始向右运动直至末速为零所需的时间是1s;
(2)导体棒从t=0时刻开始向右运动直至末速为零时离左端的距离是0.5m;
(3)前2秒内无电流,后2秒内电流方向:顺时针方向,电流大小为0.1A.
(4)4s内回路产生的焦耳热是0.02J.
