设b>a>0证明:
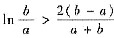 .
.
参考答案:[证法一]
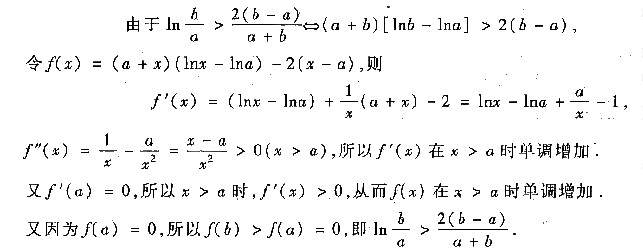
[证法二] 由于b>a>0时,

令g(t)=(t+1)lnt-2(t-1)(t≥1),则
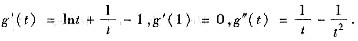 当t>1时,g"(t)>0,所以g’(t)单调递增,从而当t>1时,g’(t)>0,故g(t)单调递增,又g(1)=0,所以g(C)>g(1)=0,从而(c+1)lnc>2(c-1)(C>1).
当t>1时,g"(t)>0,所以g’(t)单调递增,从而当t>1时,g’(t)>0,故g(t)单调递增,又g(1)=0,所以g(C)>g(1)=0,从而(c+1)lnc>2(c-1)(C>1).
解析: 此题利用中值定理无法得出要证明的不等式,故选择利用单调性完成.
设b>a>0证明:
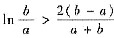 .
.
参考答案:[证法一]
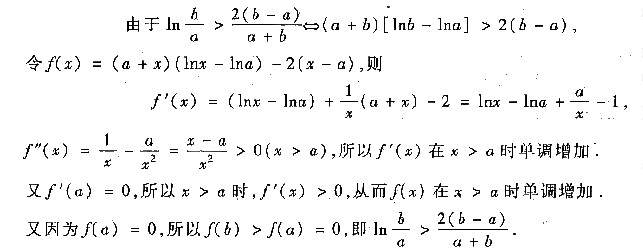
[证法二] 由于b>a>0时,

令g(t)=(t+1)lnt-2(t-1)(t≥1),则
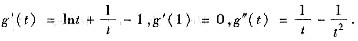 当t>1时,g"(t)>0,所以g’(t)单调递增,从而当t>1时,g’(t)>0,故g(t)单调递增,又g(1)=0,所以g(C)>g(1)=0,从而(c+1)lnc>2(c-1)(C>1).
当t>1时,g"(t)>0,所以g’(t)单调递增,从而当t>1时,g’(t)>0,故g(t)单调递增,又g(1)=0,所以g(C)>g(1)=0,从而(c+1)lnc>2(c-1)(C>1).
解析: 此题利用中值定理无法得出要证明的不等式,故选择利用单调性完成.