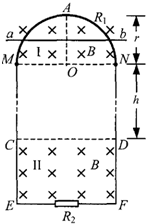
如图所示,竖直平面内有一半径为r、内阻为R1、粗细均匀的光滑半圆形金属环,在M、N处与相距为2r、电阻不计的平行光滑金属轨道ME、NF相接,EF之间接有电阻R2,已知R1=12R,R2=4R.在MN上方及CD下方有水平方向的匀强磁场I和II,磁感应强度大小均为B.现有质量为m、电阻不计的导体棒ab,从半圆环的最高点A处由静止下落,在下落过程中导体棒始终保持水平,与半圆形金属环及轨道接触良好,两平行轨道中够长.已知导体棒ab下落r/2时的速度大小为v1,下落到MN处的速度大小为v2.
(1)求导体棒ab从A下落r/2时的加速度大小.
(2)若导体棒ab进入磁场II后棒中电流大小始终不变,求磁场I和II之间的距离h和R2上的电功率P2.
(3)当导体棒进入磁场II时,施加一竖直向上的恒定外力F=mg的作用,求导体棒ab从开始进入磁场II到停止运动所通过的距离和电阻R2上所产生的热量.
(1)以导体棒为研究对象,棒在磁场I中切割磁感线,棒中产生产生感应电动势,导体棒ab从A下落
时,导体棒在重力与安培力作用下做加速运动,由牛顿第二定律,得r 2
mg-BIL=ma,式中l=
r3
I1=Blv1 R并1
R并1=
=4R8R×(4R+4R) 8R+4R+4R
由以上各式可得到:a=g-3B2r2v1 4mR
(2)当导体棒ab通过磁场II时,若安培力恰好等于重力,棒中电流大小始终不变,即mg=BI×2r
I2=
,2Brv3 R并2
公式中:R并2=
=3R12R×4R 12R+3R
解得:v3=
=mgR并2 4B2r2 3mgR 4B2r2
导体棒从MN到CD做加速度为g的匀加速直线运动,有
-v 23
=2ghv 22
得:h=
-9m2gR2 32B4r4 v 22 2g
此时导体棒重力的功率为
PG=mgvt=3m2g2R 4B2r2
根据能量守恒定律,此时导体棒重力的功率全部转化为电路中的电功率,即
P电=P1+P2=PG
所以P2=
PG=3 4 9m2g2R 16B2r2
(3)由动量定理得:-B
×2r×t=0-mv3. I
即:-B
×2r×t=-mv3B×2r× . v R并2
即:-
x=-mv34B2r2 R并2
联立,解得:x=9m2gR2 16B4r4
停下来的过程中,重力做正功,外力和安培力做负功,由动能定理得:
mgx-Fx-W外=0-
m1 2 v 23
所以产生的总热量为:Q=W外=
m1 2 v 23
在电阻上产生的热量为:Q2=
Q=3 4 27m3g2R2 128B4r4
答:(1)导体棒ab从A下落r/2时的加速度a=g-
;(2 )h=3B2r2v1 4mR
-9m2gR2 32B4r4
,P2=v 22 2g
;(3)停止运动所通过的距离 x=9m2g2R 16B2r2
,在电阻上产生的热量为 Q2=9m2gR2 16B4r4
.27m3g2R2 128B4r4
