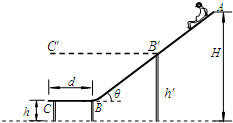
水上滑梯可简化成如图所示的模型:倾角为θ=37°斜滑道AB和水平滑道BC平滑连接(设经过B点前后速度大小不变),起点A距水面的高度H=7.0m,BC长d=2.0m,端点C距水面的高度h=1.0m.一质量m=50kg的运动员从滑道起点A点无初速地自由滑下,运动员与AB、BC间的动摩擦因数均为μ=0.1.(取重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8,运动员在运动过程中可视为质点)
(1)求运动员沿AB下滑时加速度的大小a;
(2)求运动员从A滑到C的过程中克服摩擦力所做的功W和到达C点时速度的大小υ;
(3)保持水平滑道端点在同一竖直线上,调节水平滑道高度h和长度d到图中B′C′位置时,运动员从滑梯平抛到水面的水平位移最大,求此时滑道B′C′距水面的高度h′.
(1)运动员沿AB下滑时,受力情况如图所示
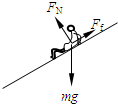
Ff=μFN=μmgcosθ
根据牛顿第二定律:mgsinα-μmgcosθ=ma
得运动员沿AB下滑时加速度的大小为:
a=gsinθ-μgcosθ=5.2 m/s2
(2)运动员从A滑到C的过程中,克服摩擦力做功为:
W=μmgcosθ(
)+μmgd=μmg[d+(H-h)cotθ]=μmg×10=500JH-h sin37°
由动能定理得:mg(H-h)-W=
mv2 1 2
得运动员滑到C点时速度的大小 v=10m/s
(3)在从C点滑出至落到水面的过程中,运动员做平抛运动的时间为t,
h’=
gt2,t=1 2 2h′ g
下滑过程中克服摩擦做功保持不变W=500J
根据动能定理得:mg(H-h’)-W=
mv2,v=1 2 2g(H-h′)- 2W m
运动员在水平方向的位移:x=vt═
•2g(H-h′)- 2W m
=22h′ g
=2-h′2+6h′ -(h′-3)2+9
当h’═3m时,水平位移最大;
答:(1)运动员沿AB下滑时加速度的大小a为5.2m/s2;
(2)运动员从A滑到C的过程中克服摩擦力所做的功W为500J,到达C点时速度的大小为10m/s;
(3)滑道B′C′距水面的高度h′为3m.
