问题
选择题
如图所示,一个内壁光滑的绝缘细直管竖直放置.在管子的底部固定一电荷量为Q(Q>0)的点电荷.在距离底部点电荷为h2的管口A处,有一电荷量为q(q>0)、质量为m的点电荷由静止释放,在距离底部点电荷为h1的B处速度恰好为零.现让一个电荷量为q、质量为3m的点电荷仍在A处由静止释放,已知静电力常量为k,重力加速度为g,则该点电荷( )
A.运动到B处的速度为零
B.在下落过程中加速度逐渐减小
C.运动到B处的速度大小为2 3 3g(h2-h1)
D.速度最大处与底部点电荷距离为kQq mg 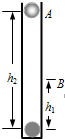
答案
点电荷在下落中受重力和电库仑力,由动能定理可得:
mgh+WE=0;
即WE=-mgh;
当小球质量变为3m时,库仑力不变,故库仑力做功不变,由动能定理可得:
3mgh-mgh=
mv2; 1 2
解得:v=2 3
;故C正确,A错误;3g(h2-h1)
由题意知,小球应先做加速运动,再做减速运动,即开始时重力应大于库仑力;而在下落中,库仑力增大,故下落时加速度先减小,后增大;故B错误;
当重力等于库仑力时,合力为零,此时速度最大,F库=3mg=
,解得:r=kQq r2
,故D错误;kQq 3mg
故选C.
