问题
问答题
设f(x)在x≥a时连续，在x＞a时可导，又
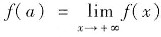，证明：存在ξ∈(a，+∞)使f’(ξ)=0．
答案
参考答案：[证] 若f(x)在x≥a时恒为常数，则显然成立．
若f(x)在x≥a时不恒为常数，则一定存在一点c∈(a+∞)，使得f(C)≠f(a)．不妨假设f(C)＞f(a)，由于
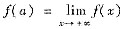，根据极限的保号性质可得：存在b＞c，当x≥b时，恒有f(x)＜f(C)，所以f(x)必在区间[a，b]内取到最大值，不妨设x0∈(a，b)使f(x0)为最大值．
所以f’(x0)=0，即方程f’(x)=0在(a，+∞)内至少有一个实根．